Membrane Modes of the String Bed
The second type of vibrational modes in a tennis racket involve only the string-bed; the frame is essentially fixed in place while the strings move together in a manner very similar to that of a circular membrane. In fact, the usual manner of identifying the modes of the string-bed is to classify them according to the number of circular and diameter nodes. The modal identification (m,n) indicates the number of diameters (m) and the number of circles (n). String-bed membrane modes contribute to the sound that the racket makes when it strikes a ball. Several of the string-bed modes - especially the (0,1) and (0,2) modes - are important to determining the ball-racket dwell time and racket power. However, since the string-bed membrane modes do not involve vibration of the handle, they have very little influence on the perception of feel in the hands of the player. These string-bed modes will be strongly damped by the popular string dampers (which - by the way - have absolutely no effect on reducing vibration in the handle).
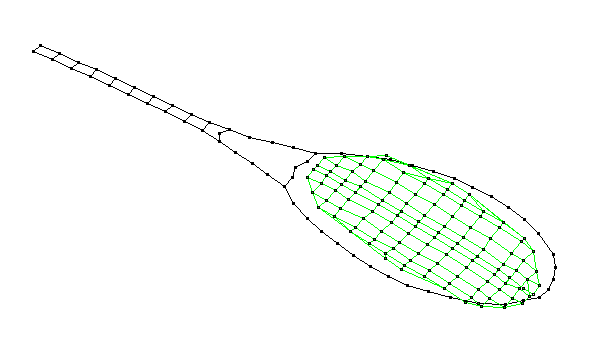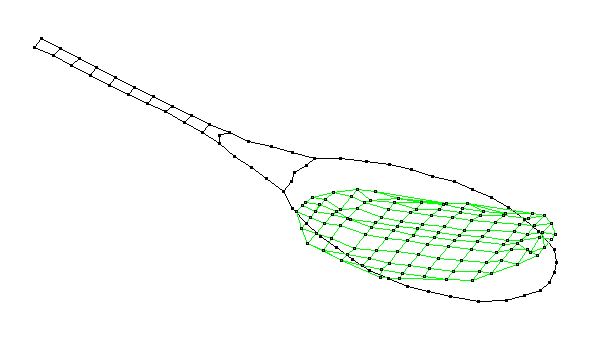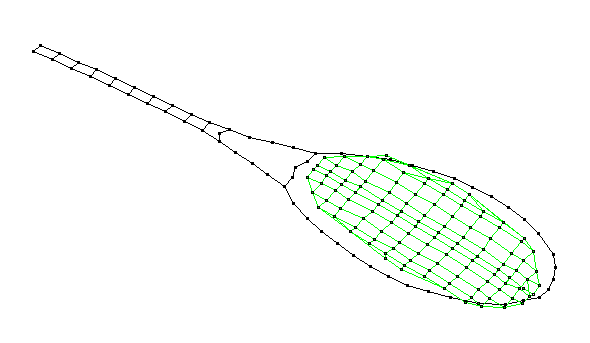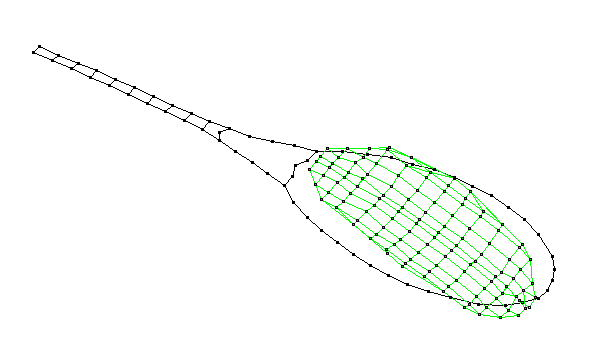
Membrane (0,1) - 582 Hz
_582.gif)
The (0,1) membrane mode has one circular node - the outer rim of the string-bed where it attaches to the frame. The entire string-bed moves as a single system. The frequency of this mode shape is highly dependent on the tension in the strings, and this shape (and its frequency) are directly related to the power of the racket, since the period of vibration (inverse of the frequency) strongly affects the dwell-time of the ball as it impacts the racket.
Membrane (0,2) - 1397 Hz
_1397.gif)
The (0,2) membrane mode has two circles, the outer rim at the frame, and a second circular node so that the inner and outer portions of the string-bed oscillate with opposite phase. This mode has a high enough frequency (short enough period) that it probably does not contribute much to racket-ball interaction.
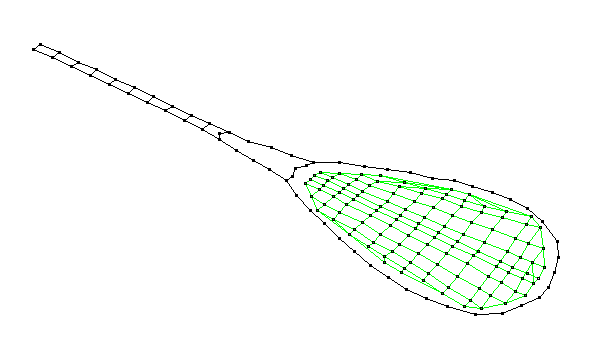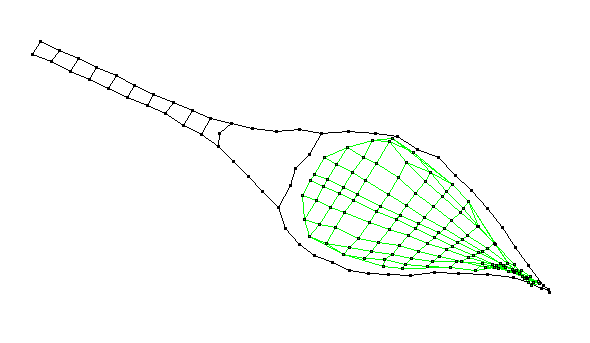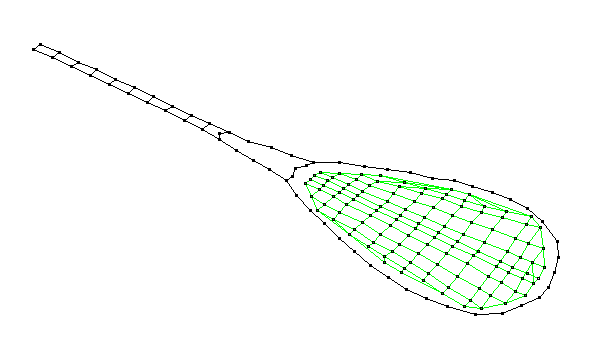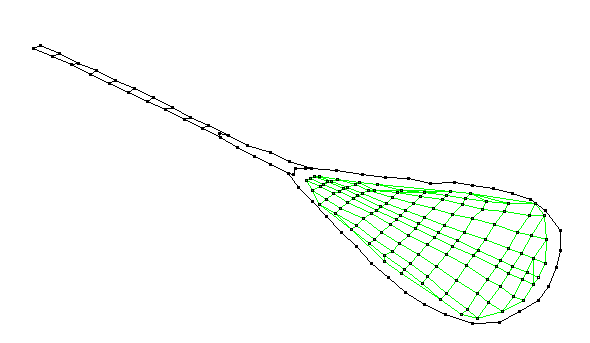
Membrane (1,1)a - 936 Hz
a_936.gif)
The (1,1) membrane has one diameter and one circle (the outer rim). In a uniform circular membrane, the (1,1) mode is actually a pair of degenerate modes, with the orientation of the diagonal rotated by 90 degrees. In an oval-shaped membrane, as is the case for the tennis racket head, the two orientations are not degenerate but have different frequencies.  The lower of the pair, denoted (1,1)a has - in this case - the diameter as a diagonal node line across the string bed.
The lower of the pair, denoted (1,1)a has - in this case - the diameter as a diagonal node line across the string bed.
Membrane (1,1)b - 996 Hz
b_996.gif)
 The higher frequency of the (1,1) split pair for the oval-shaped string bed has the nodal diameter lying along the long axis of the racket head. Because both of the (1,1) orientations have a nodal line passing through the center of the head, they do not play a very important role for impacts near the sweet spot. These modes will contribute to the "ping" sound that you hear when you tap the racket on the strings.
The higher frequency of the (1,1) split pair for the oval-shaped string bed has the nodal diameter lying along the long axis of the racket head. Because both of the (1,1) orientations have a nodal line passing through the center of the head, they do not play a very important role for impacts near the sweet spot. These modes will contribute to the "ping" sound that you hear when you tap the racket on the strings.
Membrane (2,1)a - 1300 Hz
a_1301.gif)
The (2,1) mode has two diameters and one circle. This mode shape would also be degenerate for a circular membrane, but is split for a tennis racket because of the oval shape of the head.  The lower frequency of this pair, designated (2,1)a, has one nodal diameter along the long axis of the racket, and the other at right angles across the width.
The lower frequency of this pair, designated (2,1)a, has one nodal diameter along the long axis of the racket, and the other at right angles across the width.
Membrane (2,1)b - 1301 Hz
b_1301.gif)
 The higher frequency (2,1)b mode has two diameters, making an "X" on the string-bed. Because the (2,1) modes have nodal lines crossing the center of the head, they will not be excited by impacts at the sweet spot in the center of the head.
The higher frequency (2,1)b mode has two diameters, making an "X" on the string-bed. Because the (2,1) modes have nodal lines crossing the center of the head, they will not be excited by impacts at the sweet spot in the center of the head.
Membrane (3,1)a - 1546 Hz
a_1546.gif)
The final pair of membrane modes are the (3,1) pair with three nodal diameters and six alternating regions where the string bed oscillates with opposite phase.  The mode with the lower frequency has a nodal diameter aligned with the long axis of the racket.
The mode with the lower frequency has a nodal diameter aligned with the long axis of the racket.
Membrane (3,1)b - 1578 Hz
b_1578.gif)
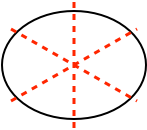 The higher frequency mode of the (3,1) pair has a nodal diameter across the width of the racket head.
The higher frequency mode of the (3,1) pair has a nodal diameter across the width of the racket head.
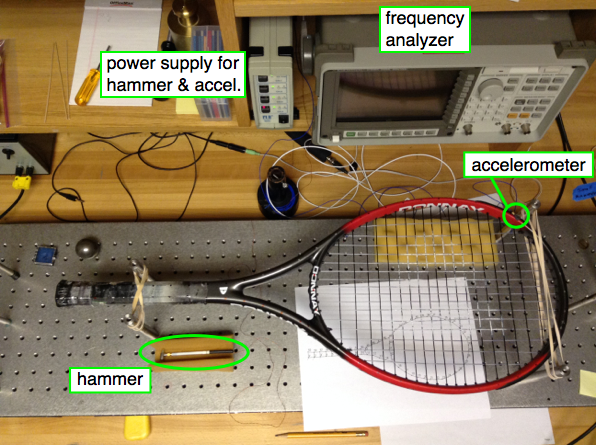 Experimental Modal Analysis (EMA) is an experimental method for extracting vibrational mode shapes, resonance frequencies, and damping rates for a structure. The experiment involves tapping the structure (in this case, a tennis racket) with a special hammer that has a force transducer in the tip to measure the impact force as a function of time. The resulting vibration response of the structure to this impact is measured with a small accelerometer attached to the structure. A two-channel frequency analyzer is used to capture the force and acceleration time signals and transform them to frequency spectra. The ratio of acceleration output to force input is called a Frequency Response Function, and is a complex quantity (in the frequency domain) whose real and imaginary parts provide the frequencies and the damping rates, and the amplitude and phase information necessary to determine the mode shapes. Using a roving impact technique, the accelerometer location is fixed, and the hammer impacts are applied at various locations on the structure - for the tennis racket data below, we used approximately a 1-inch grid spacing.
The resulting collection of Frequency Response Function data is post-processed using STAR Modal software to curve fit the FRF data, resulting in the animated shapes below.
Experimental Modal Analysis (EMA) is an experimental method for extracting vibrational mode shapes, resonance frequencies, and damping rates for a structure. The experiment involves tapping the structure (in this case, a tennis racket) with a special hammer that has a force transducer in the tip to measure the impact force as a function of time. The resulting vibration response of the structure to this impact is measured with a small accelerometer attached to the structure. A two-channel frequency analyzer is used to capture the force and acceleration time signals and transform them to frequency spectra. The ratio of acceleration output to force input is called a Frequency Response Function, and is a complex quantity (in the frequency domain) whose real and imaginary parts provide the frequencies and the damping rates, and the amplitude and phase information necessary to determine the mode shapes. Using a roving impact technique, the accelerometer location is fixed, and the hammer impacts are applied at various locations on the structure - for the tennis racket data below, we used approximately a 1-inch grid spacing.
The resulting collection of Frequency Response Function data is post-processed using STAR Modal software to curve fit the FRF data, resulting in the animated shapes below.


_582.gif)
_1397.gif)
a_936.gif)
 The lower of the pair, denoted (1,1)a has - in this case - the diameter as a diagonal node line across the string bed.
The lower of the pair, denoted (1,1)a has - in this case - the diameter as a diagonal node line across the string bed.
b_996.gif)
 The higher frequency of the (1,1) split pair for the oval-shaped string bed has the nodal diameter lying along the long axis of the racket head. Because both of the (1,1) orientations have a nodal line passing through the center of the head, they do not play a very important role for impacts near the sweet spot. These modes will contribute to the "ping" sound that you hear when you tap the racket on the strings.
The higher frequency of the (1,1) split pair for the oval-shaped string bed has the nodal diameter lying along the long axis of the racket head. Because both of the (1,1) orientations have a nodal line passing through the center of the head, they do not play a very important role for impacts near the sweet spot. These modes will contribute to the "ping" sound that you hear when you tap the racket on the strings.
a_1301.gif)
 The lower frequency of this pair, designated (2,1)a, has one nodal diameter along the long axis of the racket, and the other at right angles across the width.
The lower frequency of this pair, designated (2,1)a, has one nodal diameter along the long axis of the racket, and the other at right angles across the width.
b_1301.gif)
 The higher frequency (2,1)b mode has two diameters, making an "X" on the string-bed. Because the (2,1) modes have nodal lines crossing the center of the head, they will not be excited by impacts at the sweet spot in the center of the head.
The higher frequency (2,1)b mode has two diameters, making an "X" on the string-bed. Because the (2,1) modes have nodal lines crossing the center of the head, they will not be excited by impacts at the sweet spot in the center of the head.
a_1546.gif)
 The mode with the lower frequency has a nodal diameter aligned with the long axis of the racket.
The mode with the lower frequency has a nodal diameter aligned with the long axis of the racket.
b_1578.gif)
 The higher frequency mode of the (3,1) pair has a nodal diameter across the width of the racket head.
The higher frequency mode of the (3,1) pair has a nodal diameter across the width of the racket head.