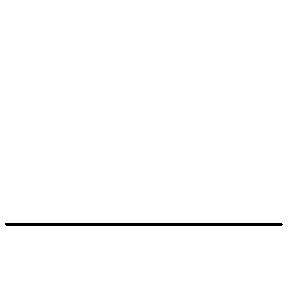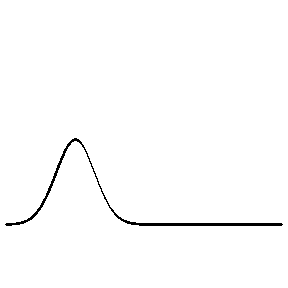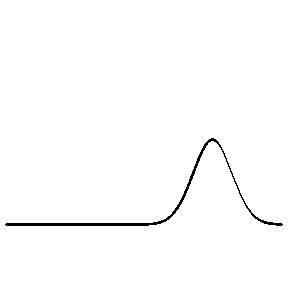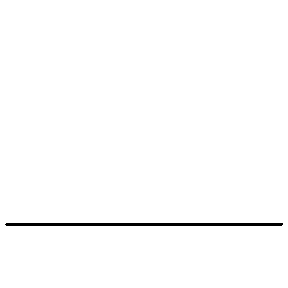Acoustics and Vibration Animations

Daniel A. Russell, Graduate Program in Acoustics, The Pennsylvania State University

Creative Commons LicenseThis work by Dan Russell is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
Based on a work at http://www.acs.psu.edu/drussell/demos.html. Additional information about using this content is available at http://www.acs.psu.edu/drussell/Demos/copyright.html.

The content of this page was originally posted on March 21, 1997. The HTML code was modified to be HTML5 compliant on March 18, 2013.

Reflection of Waves from Boundaries

These animations were inspired in part by the figures in chapter 6 of Introduction to Wave Phenomena by A. Hirose and K. Lonngren, (J. Wiley & Sons, 1985, reprinted by Kreiger Publishing Co., 1991)

When an object, like a ball, is thrown against a rigid wall it bounces back. This "reflection" of the object can be analyzed in terms of momentum and energy conservation. If the collision between ball and wall is perfectly elastic, then all the incident energy and momentum is reflected, and the ball bounces back with the same speed. If the collision is inelastic, then the wall (or ball) absorbs some of the incident energy and momentum and the ball does not bounce back with the same speed.

Waves also carry energy and momentum, and whenever a wave encounters an obstacle, they are reflected by the obstacle. This reflection of waves is responsible for echoes, radar detectors, and for allowing standing waves which are so important to sound production in musical instruments.

Wave pulse traveling on a string

transverse wave pulse traveling along a string
The animation at left shows a wave pulse travelling on a string. The speed, c, with which the wave pulse travels along the string depends on the elastic restoring force (tension, T) and inertia (mass per unit length, μ) according to

$$ c = \sqrt{T/\mu} $$

Reflection from a HARD boundary

animation of wave pulse reflecting from hard boundary
The animation at left shows a wave pulse on a string moving from left to right towards the end which is rigidly clamped. As the wave pulse approaches the fixed end, the internal restoring forces which allow the wave to propagate exert an upward force on the end of the string. But, since the end is clamped, it cannot move. According to Newton's third law, the wall must be exerting an equal downward force on the end of the string. This new force creates a wave pulse that propagates from right to left, with the same speed and amplitude as the incident wave, but with opposite polarity (upside down).
  • at a fixed (hard) boundary, the displacement remains zero and the reflected wave changes its polarity (undergoes a 180o phase change)

Reflection from a SOFT boundary

animation of wave pulse reflecting from soft boundary
The animation at left shows a wave pulse on a string moving from left to right towards the end which is free to move vertically (imagine the string tied to a massless ring which slides frictionlessly up and down a vertical pole). The net vertical force at the free end must be zero. This boundary condition is mathematically equivalent to requiring that the slope of the string displacement be zero at the free end (look closely at the movie to verify that this is true). The reflected wave pulse propagates from right to left, with the same speed and amplitude as the incident wave, and with the same polarity (right-side up).
  • at a free (soft) boundary, the restoring force is zero and the reflected wave has the same polarity (no phase change) as the incident wave

Reflection from an impedance discontinuity

When a wave encounters a boundary which is neither rigid (hard) nor free (soft) but instead somewhere in between, part of the wave is reflected from the boundary and part of the wave is transmitted across the boundary. The exact behavior of reflection and transmission depends on the material properties on both sides of the boundary. One important property is the characteristic impedance of the material. The characteristic impedance of a material is the product of mass density and wave speed, \(Z = \rho c\). 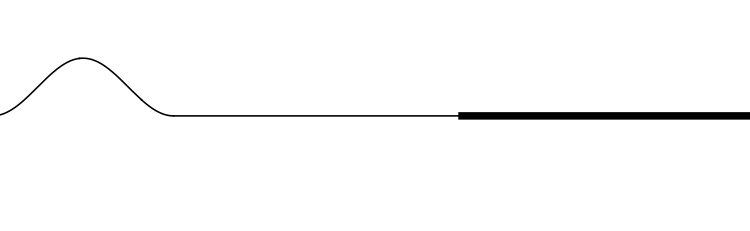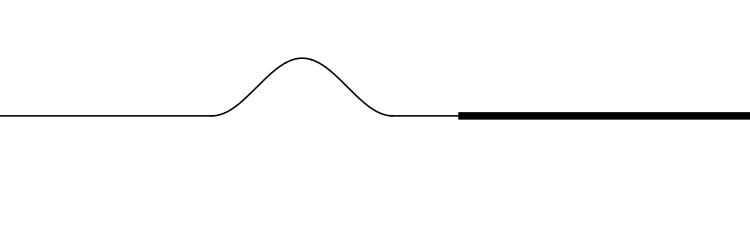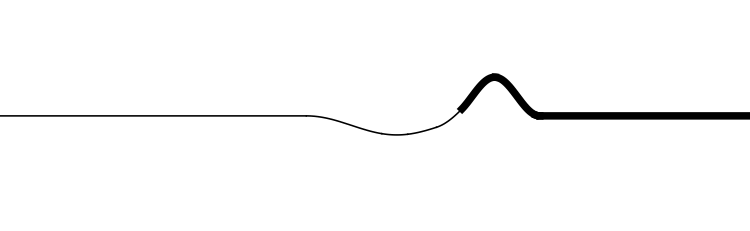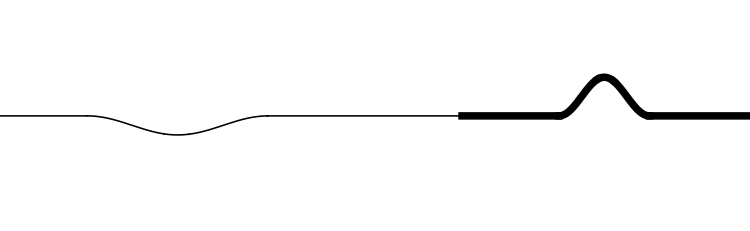If a wave with amplitude ξ1 in medium 1 encounters a boundary with medium 2, the amplitudes of the reflected wave is given by $$ \xi_r = {Z_1 - Z_2 \over Z_1 + Z_2}\xi_1 $$ and the amplitude of the wave transmitted into medium 2 is given by $$ \xi_2 = {2 Z_1 \over Z_1 + Z_2}\xi_1 $$ In the animations below, two strings of different densities are connected so that they have the same tension. The density μ of the thick string is 4 times that of the thin string.

From high speed to low speed (low density to high density)

animation of a wave pulse in a low density string reflecting from the boundary with a high density string
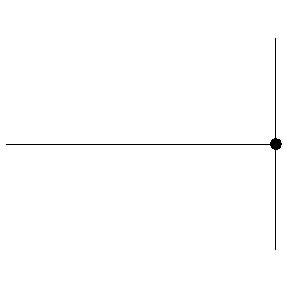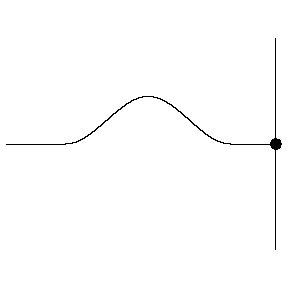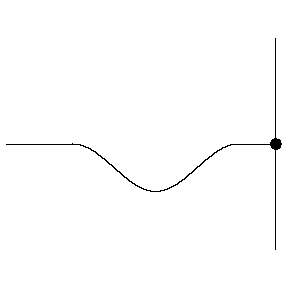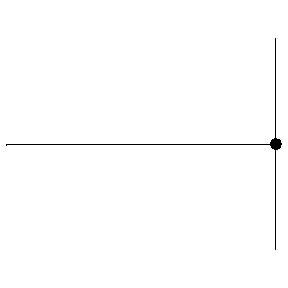
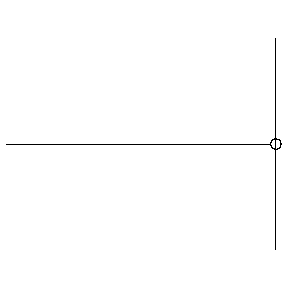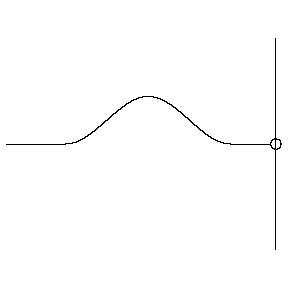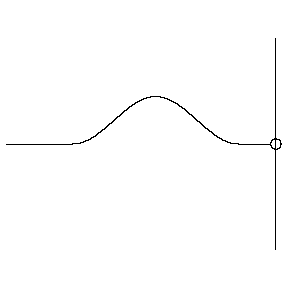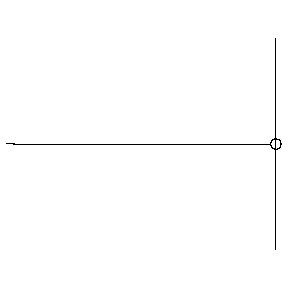
In this animation the incident wave is travelling from a low density (high wave speed) region towards a high density (low wave speed) region.
  • How do the amplitudes of the reflected and transmitted waves compare to the amplitude of the incident wave?
  • How do the orientations of the reflected and transmitted waves compare to the orientation of the incident wave? (upright or inverted?)
  • How do the widths of the reflected and transmitted waves compare to the width of the incident wave?

From low speed to high speed (high density to low density)

animation of a wave pulse in a high density string reflecting from the boundary with a low density string
In this animation the incident wave is travelling from a high density (low wave speed) region towards a low density (high wave speed) region.

  • How do the amplitudes of the reflected and transmitted waves compare to the amplitude of the incident wave?
  • How do the orientations of the reflected and transmitted waves compare to the orientation of the incident wave? (upright or inverted?)
  • How do the widths of the reflected and transmitted waves compare to the width of the incident wave?